Nodes are the essential building blocks in the Advanced interface to the Poser Material Room. They are the graphical representation of mathematical function calls, that is: calculation procedures which turn parameters (inputs) to a result (output).
Advanced
The Math group offers various nodes that can adjust and combine colors, images and other texture elements. This article discusses:
- User_defined
- Simple_color
- Colorramp
which generate colors from value inputs. See for the overview of the Math group.
User_Defined
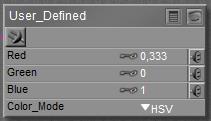 This node produces a color, that is: a three value RGB vector with each component between 0.0 and 1.0, from three independent input values.
This node produces a color, that is: a three value RGB vector with each component between 0.0 and 1.0, from three independent input values.
When Color_Mode is set to RGB, the input values are just clipped to the 0..1 range and passed through. In the HSL or HSV modes, the inputs are clipped into the 0..1 range as well, and then translated to RGB colors. For instance, Hue=0 (or 1 or 2 or …) implies Red, Hue = 0.5 implies Cyan, Hue = 0,333 is Green. The input called Red contains Hue, Green contains Saturation and Blue contains Lightness or Value respectively.
In the HSL model, the Saturation starts at 0 with grey and mixes more and more pigment into it, until it’s saturated at S=1. The taint of grey is determined by the Lightness: 0 for full black to 1 for full white. So full red requires (0,1,any) for input. In the HSV model, Saturation determines the mixture with White (0 = white, 1 = full pigment) while Value determines the mixture with Black (0= black, 1 = full pigment). Full red requires (0,1,1).
Note: a color generated by this node will not be image-driven or color swatch-driven, but value-driven. As a consequence, it will not be pre-adjusted when renders are done with Gamma Correction ON (Poser 10, or Pro all versions), and results will look brighter than for color swatches representing the same color.
Simple_Color
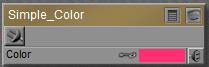 This node produces… a simple color, as set by a color-swatch. Or a simply color-filtering of anything inputted to it.
This node produces… a simple color, as set by a color-swatch. Or a simply color-filtering of anything inputted to it.
This is useful when a single color is used multiple times in a materials node tree. Now it can be defined once and managed at one place. It’s simpler than using the User_Defined node, which requires three independent input values for R,G and B separately.
But there is another serious difference: when rendering under Gamma Correction, as available from Poser 10 and Pro 2010 and up, all color swatch defined colors are affected, but numerical settings as from User_Defined are not. This might give different results for a same color, when set in different ways.
Colorramp
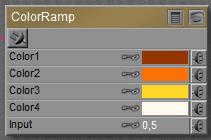 This node produces a color from a four-point gradient, having the color-points set at 0%, 33%, 66% and 100%. The interpolated color is derived from the Input value, which should be between 0.0 and 1.0. I can plug in a greyscale image in here as well, to get it colored up.
This node produces a color from a four-point gradient, having the color-points set at 0%, 33%, 66% and 100%. The interpolated color is derived from the Input value, which should be between 0.0 and 1.0. I can plug in a greyscale image in here as well, to get it colored up.
Note: when rendering with Gamma Correction, the swatches will be pre-adjusted (darkened) but each at a different rate, and the Input-value will not. As a consequence, the resulting hues produced by this node will differ, depending on whether GC is used or not. See this article for details, and for eventual solutions.
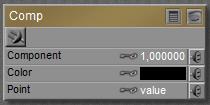 This node accepts a vector, either representing a color (Red, Green, Blue) or a pointer in space (
This node accepts a vector, either representing a color (Red, Green, Blue) or a pointer in space (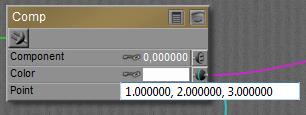 When nothing is plugged into any slot, the appropriate component of the Color swatch is passed through, the Point value is ignored, unless…
When nothing is plugged into any slot, the appropriate component of the Color swatch is passed through, the Point value is ignored, unless…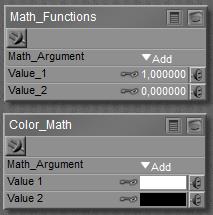 Most functions do what I can expect from them, as defined by any basic math textbook. See the Poser Reference Manual on them in case of doubt. Some operations need both inputs (like Add and Multiply), other operations work on Input_1 only (like sine, square root).
Most functions do what I can expect from them, as defined by any basic math textbook. See the Poser Reference Manual on them in case of doubt. Some operations need both inputs (like Add and Multiply), other operations work on Input_1 only (like sine, square root). The Math group offers various nodes that can adjust and combine colors, images and other texture elements.
The Math group offers various nodes that can adjust and combine colors, images and other texture elements.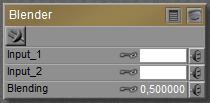 This node takes two inputs, color or image or whatever, and blends them together. When the Blending value equals 0 the result is entirely Input_1, when the value equals 1 the result is entirely Input_2, and the real blends are made by intermediate values.
This node takes two inputs, color or image or whatever, and blends them together. When the Blending value equals 0 the result is entirely Input_1, when the value equals 1 the result is entirely Input_2, and the real blends are made by intermediate values.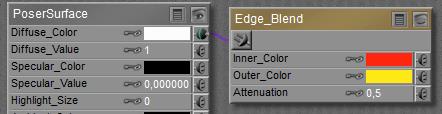 makes
makes 
 and at 0.9:
and at 0.9: 
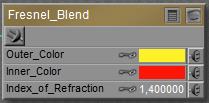 This Fresnel effect in real life concerns the balance between Reflection on one hand (high at the edges) and Refraction (with embedded Transparency, low at the edges) on the other hand. So combining Fresnel_Blend with those respective nodes is an obvious thing to do. For that reason, an explicit
This Fresnel effect in real life concerns the balance between Reflection on one hand (high at the edges) and Refraction (with embedded Transparency, low at the edges) on the other hand. So combining Fresnel_Blend with those respective nodes is an obvious thing to do. For that reason, an explicit 
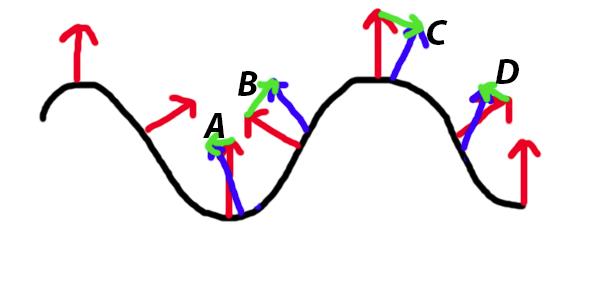




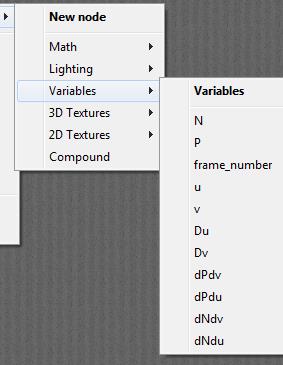
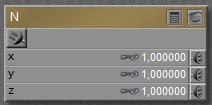 Slightly more intriguing than just single values U and V are normal N and point P:
Slightly more intriguing than just single values U and V are normal N and point P:

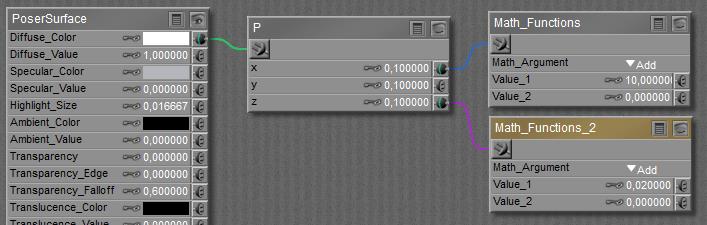


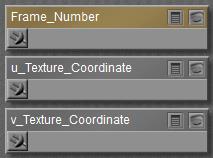 The easiest to comprehend are U, V and Frame_Number. These nodes don’t take any inputs but just report the situation in the scene: at what place on the object surface(U,V, both 0..1) at what time frame the spot is located for which the PoserSurface definition has to report on to the renderer.
The easiest to comprehend are U, V and Frame_Number. These nodes don’t take any inputs but just report the situation in the scene: at what place on the object surface(U,V, both 0..1) at what time frame the spot is located for which the PoserSurface definition has to report on to the renderer.



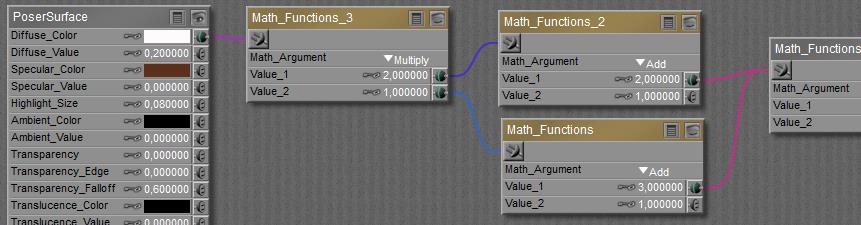
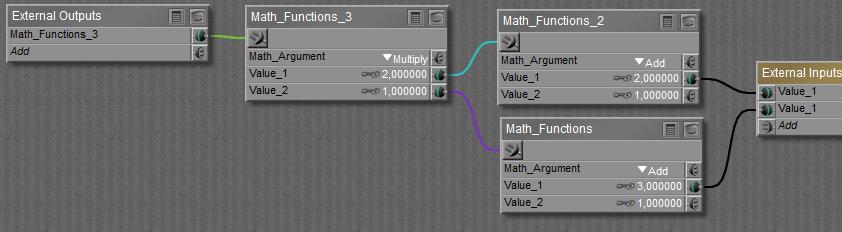
 button), and I can build a complete structure between the final node containing all External Outputs (left in the scheme below) and External Inputs (right in the scheme).
button), and I can build a complete structure between the final node containing all External Outputs (left in the scheme below) and External Inputs (right in the scheme).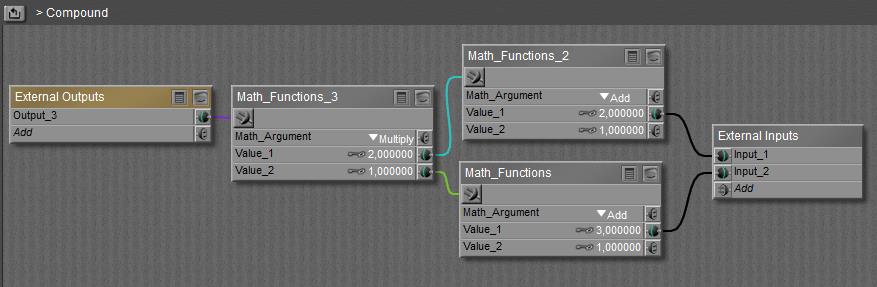
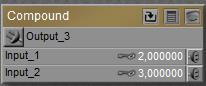 When done building the node can be collapsed (the
When done building the node can be collapsed (the  button) and will just show the outputs and inputs defined in the Material Room definition area:
button) and will just show the outputs and inputs defined in the Material Room definition area:

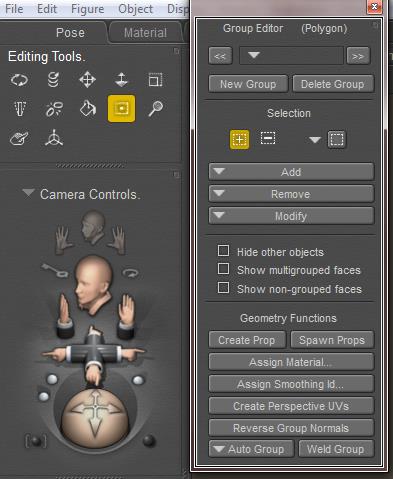 In Poser, groups are managed via the Group Editor, accessible via the Grouping Tool icon in the Editing Tools palette. The Group Editor takes a serious portion of the Figures and Props Editors chapter in the Poser Reference Manual, and reading this carefully before use is much recommended as the tool is quite powerful and can have drastic effects on the behavior of objects it’s applied to.
In Poser, groups are managed via the Group Editor, accessible via the Grouping Tool icon in the Editing Tools palette. The Group Editor takes a serious portion of the Figures and Props Editors chapter in the Poser Reference Manual, and reading this carefully before use is much recommended as the tool is quite powerful and can have drastic effects on the behavior of objects it’s applied to.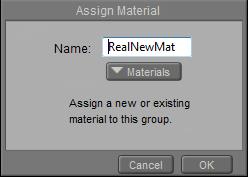 or
or